SQCスマート導入講座
第3回:管理図で工程を読む
前回までで、製品を全数検査し、その結果に基づいて不適合品率や平均不適合品率、各ロットの上方管理限界線(UCL)と下方管理限界線(LCL)を算出し、データシートを作成しました。
そして、それらの値から中心線(CL)、上側と下側の管理限界線である上方管理限界線(UCL)と下方管理限界線(LCL)を引き、さらに検査の結果を記入しました。
一般に、管理図には以下の特長があるといわれています。

- ・数字の羅列である表に比べて、図化されているためデータの可読性が高い。
- ・「あわて者の誤り」と「ぼんやり者の誤り」を防ぐ工夫がなされている(※1)。
- ・公式を使って計算ができる。
- ・時系列を追った推移や動きを継続的に監視することができる。
今回は、前回作成した管理図を用いて、工程の状態を検証します。そこから何がわかるのか、何が読み取れるのか。また、計量値の品質管理に向けたアプローチとして標準偏差や正規分布についても、少しずつ触れていきたいと思います。
- ※1「あわて者の誤り」と「ぼんやり者の誤り」
正常/異常の判断は、次の誤りを伴うとする考え方。第一種と第二種がある。
第一種「あわて者の誤り」:工程に異常はないのに異常が生じたと判断し、対策を取るという誤り。
第二種「ぼんやり者の誤り:工程に異常が生じているにもかかわらず正常と判断し、対策を取らないという誤り。
- この記事でわかること
管理図の読み方
管理図から読み取るべき最も大切な情報は「異常」です。一般に、管理図には以下の異常が現れます。
アウト(管理外れ):検査した値の点が、上方管理限界線(UCL)より上に、または下方管理限界線(LCL)より下に打点されている。
くせ(傾向):検査結果の打点位置に、一定の規則性がある。
この中で、「アウト」にはすぐ気が付きます。しかし、注意していないと「くせ」には気が付きません。
以下に、管理図中に現れる検査結果の打点パターンを示します。打点のパターンはJIS Z 9021に示されているもので、これらの傾向が現れた場合は、統計的管理状態に異変が起こっているものとし、工程の異常を疑う必要があります。
①上方管理限界線(UCL)または下方管理限界線(LCL)に打点がある
いわゆる「アウト(管理外れ)」です。検査結果の打点が、上方管理限界線(UCL)より上、または下方管理限界線(LCL)より下にある場合です。この場合、管理限界線上の点は限界内とします。
アウト(管理外れ)の例

②9個以上の打点において「連(レン)」が現れた
検査結果の打点が、中心線(CL)より上または下に、9個以上続く状態です。このような状態は「連(レン)」といわれ、異常と判断します。
連(れん)の例

③打点に傾向がある
検査結果の打点が、連続して1つの傾向を示す場合です。たとえば、連続して見られる上昇傾向や下降傾向です。この場合、6個の打点が、同一の傾向を示す場合は異常と判断します。
傾向の例

④打点が管理限界線(UCLまたはLCL)に接近している
検査結果の打点が管理限界線(UCLまたはLCL)に近い部分にある場合状態です。「管理限界線に近い部分」とは、中心線(CL)と管理限界線を3等分し、そのうち中心線に最も近い部分(C)を指します。
連続する3点中2点がAの部分にある場合、異常と判断します。
管理限界線に接近している例

⑤打点が中心線(CL)近辺に集中している
検査結果の打点が中心線(CL)に近い部分に、連続してある状態です。「中心線(CL)に近い部分」とは、中心線と管理限界線(UCLまたはLCL)を3等分し、そのうち最も中心線に近い部分(C)を指します。
一般に、Cの部分に14個以上の点がある場合は異常と判断します。この現象は他の現象と異なり、検査自体が不適切である可能性があります。たとえば、検査対象でない製品の混入していたり、測定精度の不良などが原因と考えられます。
打点が中心線近辺に集中している例

⑥打点が中心線(CL)から離れているー1
検査結果の打点が中心線(CL)から離れた部分にある状態です。「中心線(CL)から離れた部分」とは、中心線と管理限界線(UCLまたはLCL)を3等分し、そのうち中心線から遠い部分(AとB)を指します。
連続する5個の点のうち、4個がある場合は異常と判断します。
打点が中心線から離れている例ー1

Cには1個の点しかない状態(緑)
⑦打点が中心線(CL)から離れているー2
検査結果の打点が中心線(CL)から離れた部分にある状態です。前の「⑥」との違いは、Cの部分に1つも点がないことと、連続する8個の点を対象とするところです。連続する8個の点が、Cの部分にない場合は異常とします。
打点が中心線から離れている例ー2

⑧打点がジグザグ
検査結果の打点が、中心線(CL)を中心にして交互に上下する状態です。14個の打点が交互に増減している場合は異常と判断します。
打点がジグザグの例

赤枠内に14個の打点がある
管理図から工程を分析する
例として作成した管理図から工程の状態を分析します。
工程の状態は、表であるデータシートでも推し量ることができます。しかし、管理図にすることによって、直感的かつ正確な把握が可能になることがわかります。
作成した管理表を見る限り、「アウト(管理外れ)」や「連(れん)」、「管理限界への接近」および「傾向」は見られません。サンプル数の関係上、「中心線への集中」については確認できません。
また、検査値は以下のような分布になっています。
中心線に近い「Ⅲ」に:6個(●)
次に近い「Ⅱ」に:4個(■)
最も遠い「Ⅰ」に:1個(▲)
以上から、工程の管理状態に問題はないといえます。

A:上方管理限界線(UCL)B:下方管理限界線(LCL)C:中心線(CL)D:検査値E:標準偏差(σ)
ヒント:図中の「σ」について
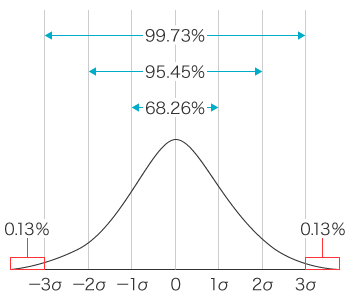
標準偏差は検査値のばらつきの度合いを示す値で、「σ(シグマ)」という記号で表します。ここでσは、各ロットの管理限界線(UCL・LCL)の値を求めたときに算出した不適合品率(p)の値のばらつきが標準偏差に相当します。その標準偏差の値を「1σ」といいます。
標準偏差のばらつきが正規分布している場合、1σには、全検査数の約68.26%が含まれます。その1σを3倍した値が「3σ」で、全検査数の99.73%が含まれます。そして、残りの0.27%が不適合品ということになります。
標準偏差の99.73%が、「平均値±3σ」の中に納まっている状態を「管理されている工程」とし、工程能力指数(cp)もこの思想で評価されています。
正規分布の例
なお、ここの例では検査ロットの数が増えていくと、不適合品率の分布は「正規分布(ガウス分布)」するようになります。正規分布に対する「1σ」や「3σ」などの値は、正規分布表として規格化され、公開されています(JIS Z 9041)。
問題点を探し出す
全体として、問題なく工程管理されていると判断できる管理図ですが、他にも工程のさまざまな状態を表現しています。ここでは、管理表が表す点や線をさらに推し量って、問題点を探ってみましょう。
検査数による不適合品率のばらつき
まず検査数について、11月3日の「206個」を最少に、最多は11月1日の「850個」と大きな差があります。この原因と数量の差と品質の関係を洗い出す必要があります。
- A:11月1日
- B:11月3日
- C:11月8日
たとえば、11月3日は「206個」を検査し不適合品率は「2.91%」、「252個」を検査した11月8日の不適合品率は「2.38%」でした。一方、「850個」を検査した11月1日の不適合品率は「2.24%」です。この傾向から、1日の検査数が
「検査台数が約250個以下、850個以上において不適合品率は増加傾向にある」
と推察できます。
検査数と不適合品率の関係

不適合品率のばらつきについて
不適合品率について、11月6日から8日以外は、すべて前日の検査に対して値が上下しています。これは、日によって設備の状態が変わっている、または材料の質が異なるなどの可能性を示唆します。
そしてこの場合、検査工程の調査はもちろん、材料を収めた前工程の検査も必要になります。また、その場合は、管理表を並べて書くなど前工程の管理図と相互に対応付けて見ることができるような工夫が大切です。
この例の場合、不適合品率のばらつきを標準偏差とするため、この偏差は特に重要な意味を持ちます。
不適合品率のばらつき

二項分布とポアソン分布を調べる
不適合品数や不適合品率などの計数値は、「離散データ」といわれます。離散データの確率の分布は「離散分布」と呼ばれる分布で表され、離散分布には「二項分布」と「ポアソン分布」があります。
二項分布
二項分布は、計数値の分布を表す代表的な手段です。たとえば、不適合品率2%の製品を10個ずつ箱に入れた場合の、1箱に不適合品が入らない確率、1個の不適合品が入る確率などの分布を表します。
以下の図はその状態を二項分布の棒グラフで表現したもので、いずれの場合も柱の高さの合計は「1」、幅も「1」になります。そして、このような分布を「二項分布」といい、その確率は以下の式で求めることができます。
- P:確率
- pr:不適合品が入る確率
- n:不適合品数
- qn−r:不適合品が入らない確率
- C:組み合わせ演算記号

二項分布は、二項式の展開や二項係数を特徴とする分布で、離散型の分布を最も明確に表現できる手法といえます。
- A:不適合品が入る確率(%)
- B:1箱に入った不適合品の数(個)
二項分布の例

ヒント:二項分布の例
二項分布の例としては、投げたコインの裏または表が出る確率です。コインの裏をp、表をqとした場合、pまたはqが出る確率は共に0.5です。コインを投げる回数を8回(n=8)とした場合の確立を計算すると、1回目が0.004、2回目が0.031、以降0.109・0.219・0.274・・・になり最後の8回目は0.004です。
たとえば1回目を求める場合、「パスカルの三角形」を用いると、計算はこのようになります。

ポアソン分布
ポアソン分布は、「離散確率分布」の1つです。「離散確率分布」とは、ぶつ切りの数値を持つ現象のパターンを確立することです。離散確率分布には、他に「ベルヌーイ分布」や「カテゴリ分布」があり、一般にベルヌーイ分布は「0か1」、といった整数の出現確率を求めることに利用され、カテゴリ分布は特定の範囲の整数の中から各数値の出現回数を求めることに利用されます。
ポアソン分布はこの式で求めることができます。

npは、試行の回数(n)と確率(p)が起こる平均値なので、np=mとすると、ポアソン分布の式はこのようになります。

たとえば、不適合品率2%の製品を30個ずつ箱に入れると、P=0.02 q=30で、m=np=0.6になります。
e−mの値はe−m=0.549なので、ポアソン分布はこのようになります。

つまり、ポアソン分布は二項分布の式をp=m=e−mとして値を固定した状態で、nの値を増やしていくか、pの値を減らしていくと、求めることができます。
ポアソン分布は、自然対数(e−m)といった高度な数学を用いますが、指数関数を使うことで求めることができます。ポアソン分布は、二項分布に比べて試行回数(n)が非常に大きく確率(p)が非常に小さいときに使われます。また、nとpが不明な場合でも使うことができる点も、二項分布と異なります。
- P(r)=ポアソン分布
- m=確率(例:n回行う間に確率(p)の事象が起こる回数の平均)
- r=試行回数
- e=自然対数*

- *自然対数(e)
ネイピア数(ネピアの数)を底に用いる対数です。「e」という文字ですが、 「2.71828・・・」という数字を用います。ネイピア数は極限値で、この式で与えることができます。

ガウス分布(正規分布)
確率の分布を示すヒストグラム(グラフ)は、その密度を高めて(検査回数を増やして)いくと、その頂点を結ぶ線は滑らかな曲線になります。そして、それは中央が高く、左右に向かって滑らかに下がっていく正規分布の曲線になります。これを「ガウス分布」といいます。ガウス曲線は、誤差を示す曲線であるため、「誤差曲線」ともいわれます。
誤差がガウス曲線を描く理由としては、たとえばある物体を測るときに発生する誤差の原因は無数で、かつ不規則です。その結果、計測値が大きくなったり小さくなったりするわけです。
それは、瓶の口から砂を入れた場合に中央を頂点とした山ができる現象と同じといわれており、瓶の中の山の形のように、誤差も分布するというのが定説となっています。
ヒストグラムからガウス分布へ

SQCに最適なセンサとは
3回にわたり、品質管理のテクニックと重要性について説明してきました。その一連の作業を通じて、品質管理にとって、サンプルの数や検査の期間、高い精度のデータの必要性も認識できました。
しかし、工場内は検査にとって良い環境とは限りません。たとえば、さまざまな照明でセンサ周辺の明るさが変化します。ライン上では乱反射するワークや低反射のワーク、位置合わせが困難なワークが流れます。
一般的なセンサが苦手とする状況でも、画像センサは、安定した検出/判別を約束します。撮像が難しいワークや照明の変化が激しい現場でも安定検出が可能。
また、位置補正機能は位置合わせの工程を不要にします。そして、設定データの保存・呼び出し機能は、段取り替えの強い味方です。

「センサでは不安、本格的な画像処理システムは不要」
画像センサは、そんなシチュエーションに最適な1台です。
- 関連ページ