Sal 最小自己相関長さ

自己相関関数について

自己相関とは、画像処理においては、画像それ自身の座標をずらした画像とどれだけ良く整合するかを測る尺度です。

Sal、Strの計算時に利用している自己相関関数は以下となります。

この関数の説明を簡易にするために、X方向のみで説明します。

まず、以下のような段差のデータがあるとします。

このデータの自己相関は以下のような形になります。

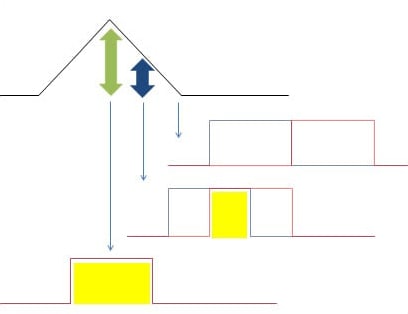
簡易に説明すると、自己相関関数は、高さデータと高さデータ自身をずらしたデータの重なる部分を求めます。(下図の黄色い領域です。)
ずらす量が小さいと、重なる部分が大きいため、自己相関も大きくなります。
ずらす量が大きいと、重なる部分が小さくなるので、自己相関も小さくなります。

急激な段差がある場合は、ずらす量がわずかであっても大きく形状が変化するため、自己相関関数がすぐに減衰します。
なだらかな形状しかない場合は、ずらす量を大きくしないと形状が変化しないので、自己相関関数はなかなか減衰しません。

Salは最も速く自己相関が減衰するまでの距離を求めるため、表面の高さが急激に変化している箇所があるか否かを判定することができます。
また、Strは最も速く自己相関が減衰するまでの距離と、最も遅く自己相関が減衰するまでの距離の比を求めるため、筋目の有無を判定することができます。