電界と電気力の基礎
物質に電流が流れる場合、そこには必ず電界が存在します。ここでは、電界とは何か?といった基礎知識から、ガウスの定理による電界の求め方まで、詳しく解説します。
電界とは
電荷とは帯電したものが持っている電気の量のことをいいます。陽子に比べて電子が多いと-、電子が少ないと+となります。記号はQ、単位はC(クーロン)で表します。2つの電荷量をQ1、Q2、距離をr[m]、両電荷間に働く力をF[N]とすると、クーロンの法則は次の式で表されます。

内側から外へ遠ざかるほど、電界強度は弱くなる。
電界(電場)とは、帯電した物体の回りに存在し、その電荷に働く力の存在する領域と考えます。例えば、ある空間に点電荷*が存在することで、その回りの空間が特別な性質を持つことになり、そこに別の点電荷を持って来ると、その空間の作用により持ち込んだ点電荷に力を作用させる、いわば「電荷の勢力範囲」と考えます。そして、その勢力は図のように、中心から遠ざかるにつれて小さくなります。この電界の強さを「電界強度」といい、図のように、中心から外側に拡がり、遠ざかるほど電界強度は弱くなります。
その性質上方向性を持つことになるので、表示にはベクトルを使用します。電界を表すには、その強さだけでなく方向も関係します。
*点電荷…大きさが測定できないような極めて小さな物体に帯電している電荷
空間に点電荷Q[C]が存在し、その電荷上に働く力をF[N]とした場合の電界強度は、
E=F/Q[V/m]
電界の単位[V/m]は単位距離あたりの電位差を表します。逆にすると、
F=QE[N]
となり、これが電界中に置かれた電荷に作用する力、つまり「クーロン力」です。
以上の数式より、点電荷の作り出す電界強度は、

電荷量Q[C]の点電荷があると、その回りの空間は電界強度は点電荷からの距離r[m]の2乗に反比例します。
電気力線
電界の方向は、プラスの電荷から出てマイナス電荷へと向かう方向になります。
電気力線とは、下図のように、電界の方向を描いた仮想の線です。電気力線の方向が電界を示し、プラス側からマイナス側に向かっています。

点電荷の電気力線

存在する電気力線
下図のように帯電体(導体)の場合は、電気力線は表面から垂直に出ています。このとき、帯電体の表面電荷が同じ密度で帯電していると、電気力線も同じ間隔になります。密度は電位の高さを示しており、電気力線の数が多く間隔が狭いところは電界が強く、逆に本数が少なく間隔が広いところでは電界が弱いことがわかります。
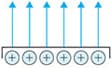
電気力線
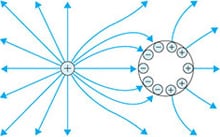
電気力線
ガウスの定理
電界にある電荷が存在するとき、その量や形状により電界を計算する方法があります。これを「ガウスの定理」といい、接近した帯電体が電界に作用する電気力を計算することで、静電気障害への対策に役立ちます。
下表は、「ガウスの定理」による計算式です。
下表の「ガウスの定理」で、電荷分布の状態に対しての点や線の回りにある電界を計算すると、帯電物の誘導率と電界強度は反比例し、電気力線の密度と電界強度は比例することが示されています。つまり、先端が尖った形状である場合、その部分の電気力密度が大きくなり、電界が高くなることになります。
| 電荷の形態 | 電荷量 | 電界[V/m] | ||
|---|---|---|---|---|
| 点電荷 | Q[C] |
E=Q/4πε0r2 |
||
| 線電荷 | λ[C/m] |
E=λ/2πε0r |
||
| 面電荷 | δ[C/m2] |
電界[V/m] |
E=σ/ε0 |
導体 |
E=σ/2ε0 |
絶縁体 |
|||
E=σ/ε0 |
導体 |
|||
E=σ/2ε0 |
絶縁体 |
|||
| 円筒 | ρ[C/m2] |
電界[V/m] |
E=ρr/2ε0 |
円筒内 |
E=a2/2rε0 |
円筒外 |
|||
E=ρr/2ε0 |
円筒内 |
|||
E=a2/2rε0 |
円筒外 |
|||
| 球 | ρ[C/m2] |
電界[V/m] |
E=ρr/3ε0 |
球内 |
E=ρa3/3ε0r2 |
球外 |
|||
E=ρr/3ε0 |
球内 |
|||
E=ρa3/3ε0r2 |
球外 |
|||
帯電体の中心からの距離:r、帯電体半径:a、真空の誘電率:ε0
【例】
1[C]の点電荷を作る電界
点電荷から電界の距離が1[m]の場合、

これは、空気中の絶縁破壊強度3×106[V/m]と比較すると、おおよそ1000倍にもなり、これは雷による放電に相当するもので、実用的ではありません。
例えば、プラスチック表面を布で摩擦したときの帯電量は単位面積あたり10-5[C/m2]程度ですので、表面に帯電している電界は以下のようになります。