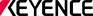カム曲線
カム曲線とは、カム本体(原動節)の輪郭形状のことではなく、フォロアから従動節を介して作動する作動端の運動曲線のことを指します。カムの動作は、カム曲線によって表現され、カム曲線には定型的な曲線から、製品の動作目的に合わせた独自の曲線まで、さまざまな形状があります。
カム曲線の種類
カム曲線には、大きく分けて
- 「変形台形曲線(MT[Modified Trapezoid]曲線)」
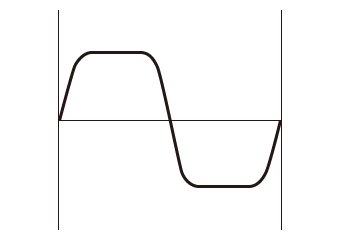
- 「変形正弦曲線(MS[Modified Sine]曲線)」
があります。いずれも縦軸がカムのリフト量、横軸がカムの回転角を示します。
その他、曲線のパラメータを変えることで目的の曲線が自由に作れる汎用カム曲線として
- 「ユニバーサルカム曲線」
- 「グローバルカム曲線」
- 「GMCV(General Modified Constant Velocity)カム曲線」
などがあり、さらに各製造メーカー独自の技術で加速度特性や入/出力特性の向上を図ったカム曲線が存在します。
カム曲線の読み方
一般にこれらのカム曲線は、横軸に「カムの回転角」、縦軸に「リフト量」を設定し、「変位曲線」・「速度曲線」・「加速度曲線」を示し、それぞれの特性を表します。これらの曲線が示す現象を「カム理論」といい、特に最も多く使われている板カムが示す特性は「板カム理論」といわれ、カム理論の基礎になっています。
ここでは、等速度カム・等加速度カム・単振動カムを例に、各カム曲線が示すカムの仕様を説明します。
等速度カムのカム曲線
等速度カムは、カムが80°回転する間に従動節は回転角に比例して変位(上昇)し、80~180°の間では上昇を停止します。この曲線からわかる等速度カムの特性は、0~80°の間で急激に加速するので、従動節に大きな負担がかかるということです。
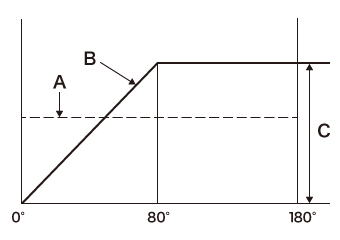
- A:速度
- B:変位
- C:リフト量
等加速度カムのカム曲線
等加速度カムは、カムが90°回転する間に従動節は加速度+aで変位(上昇)し、90°を超えると-aで減速して180°で停止します。この曲線からわかる等加速度カムの特性は、90°付近で速度変化とともに衝撃も小さくなるので、高速で回転するカムに向いているということです。
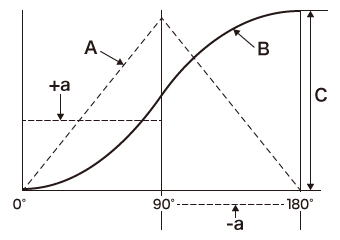
- A:速度
- B:変位
- C:リフト量
- +a:加速度プラス区間
- -a:加速度マイナス区間
単振動カムのカム曲線
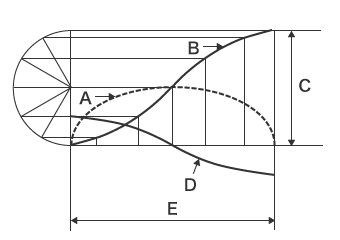
単振動カムは、従動節の変位と速度・加速度が正弦曲線になり、急激な変化はしません。この曲線からわかる単振動カムの特性は、従動節に与える衝撃が小さい理想的なカムであるということです。
- A:速度
- B:変位
- C:リフト
- D:加速度
- E:角度